Monty Hall: la paradoja que ni Erdös entendió
El problema de Monty Hall es uno de los mejores ejemplos en los que modelar un fenómeno para calcular la probabilidad de un evento es verdaderamente complicado pues desafía nuestra intuición. En este artículo vamos a explicar el famoso problema de Monty Hall y el razonamiento detrás de una simulación que convenció al mismísimo Paul Erdös después de que desafiara su intuición. Paul Erdös es seguramente uno de los matemáticos más importantes del siglo pasado.
Este célebre problema tiene su origen en un juego televisivo estadounidense llamado Let's Make a Deal, conducido por Monty Hall en las décadas de 1960 y 1970. La dinámica del programa ganó notoriedad cuando la columnista Marilyn vos Savant explicó en 1990 cuál es la estrategia correcta para ganar el concurso generando una controversia pública que incluyó cartas de cientos de matemáticos que inicialmente la contradecían, pero que luego reconocieron su razonamiento correcto.
En nuestro curso de Causalidad en Machine Learning hemos elegido este famoso problema para ilustrar tanto el razonamiento bayesiano como el razonamiento detrás de un modelo causal. Si desean más información sobre el curso que comenzó la semana anterior con gusto pueden escribirnos en Colegio de Matemáticas Bourbaki o al whatsapp de Bourbaki.
La paradoja de Monty Hall
El planteamiento del problema es bastante sencillo y las primeras dos variables aleatorias no tienen ninguna complicación. A continuación describimos las reglas del concurso:
Un concursante elige una puerta a la que llamaremos Z, esta puerta puede ser cualquiera de las tres, digamos Z= A, B o C. No es descabellado imaginar que después de un histórico los concursantes elegirán con la misma probabilidad 1/3 cualquiera de las tres puertas. Desafortunadamente no sé si esta base de datos exista, ¡pero sería muy interesante encontrarla!
En alguna de estas puertas hay un premio, denotaremos por la letra W al lugar donde se encuentra el premio, es decir también W= A, B o C. Nuevamente podríamos suponer que los organizadores del concurso no tienen alguna preferencia particular pero esto solo lo podríamos comprobar revisando la base de datos histórica.
Hasta el momento solo estamos considerando dos variables aleatorias Z y W que tampoco parece descabellado imaginar que son independientes entre sí. De nuevo hay algo que podríamos calcular estadísticamente si tenemos la base de datos.
Hechas las hipótesis anteriores podríamos suponer que la base de datos histórica se ve más o menos de la siguiente manera:
A partir de aquí el problema se va a comenzar a complicar:
Una vez que tanto el concursante como el programa han elegido la puerta donde cree que está el premio y está el premio respectivamente, Monty Hall elegirá una puerta y la abrirá, de nuevo MH= A, B o C. Existen dos reglas que no podemos alterar para la variable MH:
Si el concursante ha elegido una puerta Z, Monty Hall no puede abrir esa puerta.
Si el premio ha sido colocado en W, Monty Hall no puede abrir esa puerta.
Estas reglas duras establecen una poderosa relación entre las siguientes variables:
Una vez que conocemos el valor de Z, la probabilidad de la variable MH se modifica.
Una vez que conocemos el valor de W, la probabilidad de la variable MH se modifica.
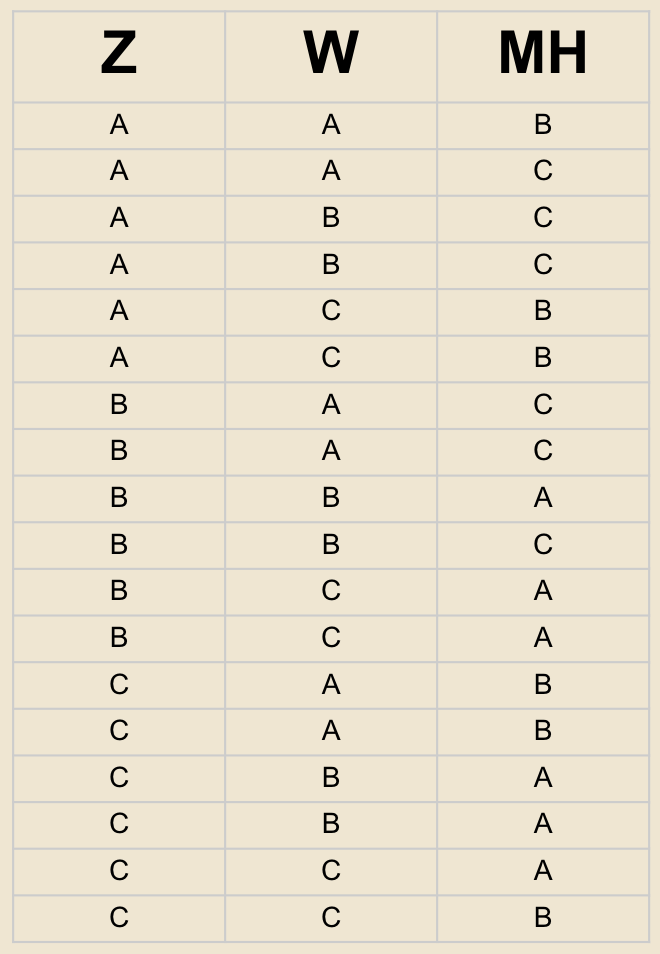
Después de estas consideraciones podríamos suponer que la siguiente base de datos representa una simulación de la interacción entre las tres variables anteriores suponiendo que si el premio W y la elección del concursante Z son iguales, entonces MH se modelará como una distribución de Bernoulli uniforme.
Es importante notar que en algunos casos los registros parecen repetidos lo cual se debe a lo siguiente: si suponemos que las variables Z y W son independientes, entonces las siguientes probabilidades marginales deberán de ser iguales a un noveno:
Si bien Monty Hall tiene el 50% de posibilidades para elegir B o C en el primer caso (cuando tanto Z como W valen A), en el segundo caso (cuando Z= A y W=B) solo podría elegir a C, lo cual nos obliga en nuestra simulación a incluir dos veces el caso (A,B,C).
Después de estudiar esta base de datos lo que nos podemos preguntar es lo siguiente: ¿en cuántos casos de esa simulación le conviene cambiarse al concursante? La respuesta correcta es que en dos terceras partes de los casos posibles, al concursante le convendría cambiarse de puerta una vez que conozca el valor de MH.
Es posible estudiar este mismo problema desde un punto de vista bayesiano o causal sin embargo eso lo reservaremos para otra ocasión.
¿Dónde aprender sobre causalidad?
En el Colegio Bourbaki estamos por comenzar nuestro flamante curso sobre la Causalidad en Machine Learning, pueden conocer más detalles sobre el temario en esta liga. Si tienen más dudas también nos puede escribir al whatsapp de Bourbaki.
Track de Ciencia de Datos (Julio 2025, 49 semanas).
Les compartimos algunas notas, presentaciones y clases muestra del curso en el siguiente link. De igual manera los invitamos a conocer el Temario del curso de 49 semanas.
Aquí pueden asistir virtualmente a la sesión informativa con el Director del Track de Ciencia de Datos. En esta sesión se tratan los conocimientos previos necesarios para inscribirse en nuestro curso, las dinámicas de las clases así como los objetivos finales a los que aspiran nuestros estudiantes al graduarse de este programa.
Track de Ciencia de Finanzas Cuantitativas (Julio 2025, 49 semanas).
Les compartimos algunas notas, presentaciones y clases muestra del curso en el siguiente link. De igual manera los invitamos a conocer el Temario del curso de 49 semanas.